|
|
||||||||||||||||||||
  School of Computational Sciences CAMP Home People Research Simulation gallery ├ Hurricane predictions ├ Higher-order upwind schemes on unstructured meshes ├ Urban scale simulation └ Advanced statistical methods (neural networks) Publications Resources for students Data archive Annual conference Computing resources Related links About our webpage Contact us |
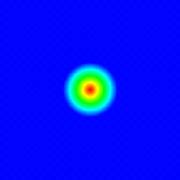
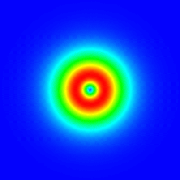
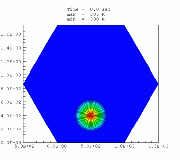
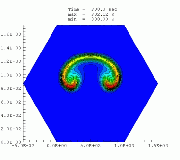
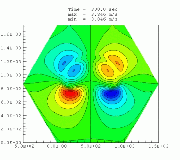
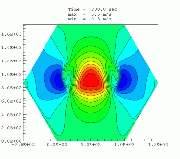
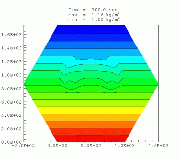
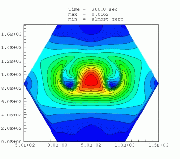
Higher-order upwind schemes on unstructured meshesHigher-order finite volume solvers have been developed for the atmospheric transport equation as well as the Navier-Stokes equations. The solver is based on unstructured triangular grids in two dimensions. Different gradient reconstruction techniques have been tested to achieve higher-order accuracy in space and various slope limiters have been implemented to enforce monotonicity. Higher-order accuracy in time is maintained with the help of multi-stage Runge-Kutta explicit time-marching. Solution-adaptive techniques have also been used to demonstrate the computational efficiency associated with the use of unstructured grids.a. Smolarkiewicz's Deformational Flow Top left: Initial tracer field, top right: Initial flow field (streamfunction), bottom left: Tracer field at 1000 iterations, bottom right: Tracer field at 3000 iterations.
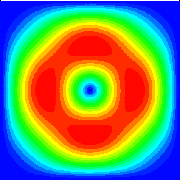
For a description of this test case see: Smolarkiewicz, P. K., 1982: The multi-dimensional Crowley advection scheme. Mon. Wea. Rev., 113, 1050-1065. b. Doswell's Frontogenesis Top left: Initial tracer field, top right: Initial flow field (wind speed), bottom left: Numerical solution at time = 4 units, bottom right: Exact solution at time = 4 units.
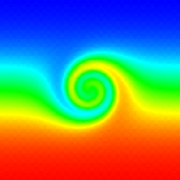
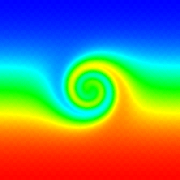
For a description of this test case see: Doswell, C., 1984: Kinematic Analysis of Frontogenesis Associated with a Nondivergent Vortex. J. Atmos. Sci., 41, 1242-1248. c. LeVeque's Swirling Deformational Flow Top left: Initial tracer field, top right: Initial flow field (wind speed), bottom left: Tracer field at 2300 iterations, bottom right: Tracer field at 4500 iterations.
For a description of this test case see: LeVeque, R. J., 1996: High-resolution conservative algorithms for advection in incompressible flow. SIAM J. Numer. Anal., 33, 627-665. d. Convection in Neutral Atmosphere Top left: Initial potential temp (K), top right: potential temp. (K) after 300s, middle left: u-velocity (m/s) after 300s and middle right: v-velocity (m/s) after 300s into the simulation, bottom left: density after 300s and bottom right: Mach number after 300s into the simulation.
Atmospheric Flow Equation Set (Conservation of Energy in terms of rho-theta), Neutral Atmosphere in hydrostatic balance initially, Warm bubble added near the lower boundary - Velocities set to zero initially, Godunov Method with the HLLC Approximate Riemann Solver, 2D Unstructured Triangular Mesh, All boundaries treated as solid wall See the
contact
page for detailed
information on
contacting us. |
|||||||||||||||||||